[자료구조] Trie 구조 (트라이)의 개념과 구현방법을 알아보자 (접두사 트리)

#알고리즘 #자료구조

트라이(Trie)

Trie는 문자열 집합을 표현과 검색에 특화된 트리 구조의 자료구조입니다. Trie를 이용하면 검색하려는 문자열의 길이를 M이라 할때 문자열을 O(M)시간에 검색할 수 있습니다. 만약 배열에서 특정 문자열을 찾고자 한다면 O(N)만큼의 시간이, 이진 탐색을 하더라도 O(logN)시간이 필요합니다. 이에 비하면 Trie 구조는 문자열 검색에 있어 문자열의 길이만큼 소모 되므로 문자열 검색에 매우 특화되어 있음을 알 수 있습니다.

구조

구현을 하기전에 개념부터 알아보겠습니다. 루트 노드는 어떠한 단어도 가지지 않고 루트 노드의 아래부터 문자열의 접두사(prefix) 가 하나씩 이어지게 됩니다. 이러한 특징때문에 Trie는 접두사 트리(Prefix Tree)라고 불리기도 합니다.

{ 
    "ABSORB", 
    "ABSORBED" , 
    "ABSTRACT", 
    "ABSTENTION", 
    "ACCESS", 
    "ACCESSIBLE", 
    "GOOD", 
    "GOODNESS", 
    "GOOGLE"
} 

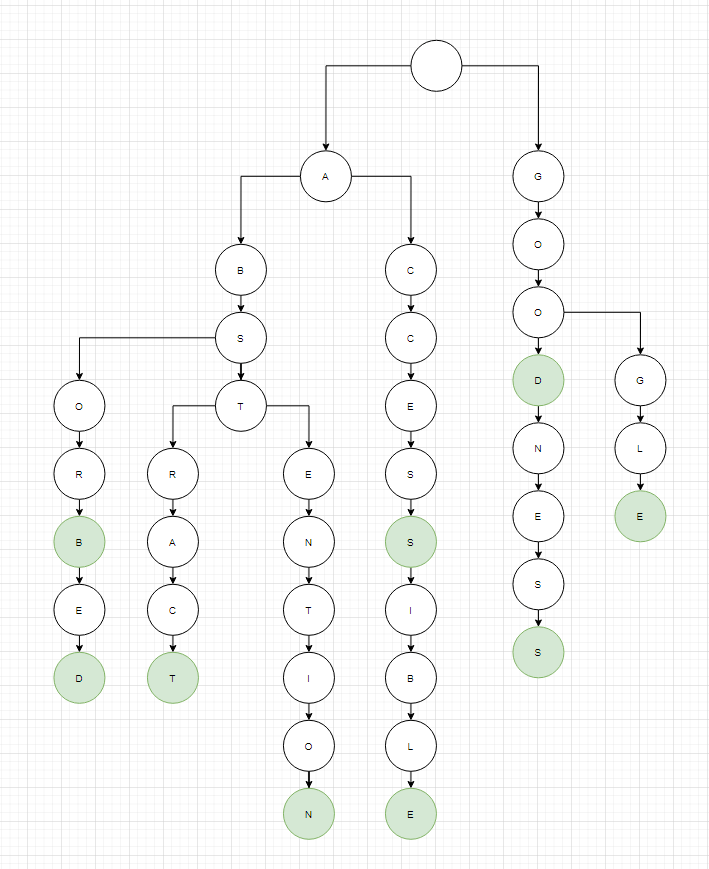
위의 문자열 집합을 가지고 있다고 가정할 때 아래의 그림은 Trie를 시각화한 것입니다. 아래에 그림에서 연두색 노드는 문자열의 말단을 의미합니다. 즉, 루트 노드의 자식노드 부터 연두색의 노드까지의 접두사들이 모여 하나의 단어를 이루게 되는 것입니다.

구현

개념을 알아보았으니 구현을 해보도록 하겠습니다. Trie구조에 노드가 되는 부분 부터 정의하도록 합시다.

#define N_ALPHABATS 26
-----------------------------
TrieNode* child[N_ALPHABATS];
bool isTerm;

앞서 설명한 개념과 같이 위의 두개의 맴버 변수만 가지면 됩니다. 자식노드를 담고 있는 child 배열은 26의 길이를 가지며 이는 알파벳의 개수로 숫자 집합의 문자열을 가진다면 0~9까지 길이 10과 같이 적절한 길이를 주면 됩니다. isTerm은 bool 타입으로 단어의 말단여부를 나타내고 true라면 단어의 끝이 됩니다. 위의 그림에서 초록색 노드가 true인 경우입니다. 따라서 위의 그림에서도 ABSTEN이 Trie에 포함되지만 ABSTEN의 말단인 N이 Trie의 말단이 아니기때문에 단어가 아니라는 것을 의미합니다.

#define N_ALPHABATS 26

class TrieNode {
public:
    TrieNode* child[N_ALPHABATS];
    bool isTerm;

    TrieNode() {
        isTerm = false;

        for (int i = 0; i < N_ALPHABATS; i++) {
            child[i] = NULL;
        }
    }

    ~TrieNode() {
        for (int i = 0; i < N_ALPHABATS; i++) {
            if (child[i] != NULL) {
                delete child[i];
            }
        }
    }

    int toNum(char c) {
        return tolower(c) - 'a';
    }

    void insert(const char* words) {
        if (*words == '\0') {
            isTerm = true;
            return;
        }

        int next = toNum(*words);

        if (child[next] == NULL) {
            child[next] = new TrieNode;
        }

        child[next]->insert(words + 1);
    }

    bool find(const char* words) {
        if (*words == '\0') {
            return isTerm;
        }

        int next = toNum(*words);
        if (child[next] == NULL) {
            return false;
        }

        return child[next]->find(words + 1);
    }
};

생성자에서 isTerm을 false로, child는 모두 NULL로 초기화 합니다. 소멸자에서는 동적할당한 메모리를 해제합니다. toNum(char c) 메서드는 A~Z 까지 대소문자를 구분하지 않고 0 ~ 25로 대응시킵니다. 이 메서드는 각 알파벳의 자식 노드가 있는 배열의 인덱스를 찾기 위해 필요합니다.

void insert(const char* words) 메서드는 단어의 각 접두사를 자식노드에 하나씩 추가하고 단어의 말단 부분에서는 isTerm을 true로 표시하여 단어의 끝임을 나타냅니다. 접두사에 해당되는 자식노드가 NULL이라면 새로 할당합니다. word + 1은 포인터로 현재 word다음의 접두사인 문자를 가리케 됩니다. 예를 들면 GOOD에서 word가 가리키는 부분이 G라면 word + 1은 char 사이즈 만큼 다음 주소를 가리키므로 O가 됩니다. 이를 반복하면 Trie에 새로운 단어를 추가할 수 있습니다.

bool find(const char* words) 메서드는 Trie가 해당 문자열을 갖고 있는지 여부를 확인하여 반환합니다. 문자열 접두사를 하나씩 따라 자식노드로 이동하고 문자열의 말단 \0에서 Trie 노드의 isTerm을 반환합니다. 이는 isTerm이 true인 경우, Trie가 해당 문자열을 갖고 있다고 판단 할 수 있고 따라서 true를 반환합니다.

테스트

아래의 테스트 코드를 통해 위에서 구현한 Trie가 잘 작동하는지 확인하도록 하겠습니다.

int main(void) {
    TrieNode root;

    string words[18];

    words[0] = "ABSORB";
    words[1] = "ABSORBED";
    words[2] = "ABSTRACT";
    words[3] = "ABSTENTION";
    words[4] = "ACCESS";
    words[5] = "ACCESSIBLE";
    words[6] = "GOOD";
    words[7] = "GOODNESS";
    words[8] = "GOOGLE";
    words[9] = "ABSO";
    words[10] = "ABSOR";
    words[11] = "ABST";
    words[12] = "ABSTENT";
    words[13] = "ACCE";
    words[14] = "ACCESSIE";
    words[15] = "OD";
    words[16] = "NESS";
    words[17] = "GOGLE";

    for (int i = 0; i <= 8; i++) {
        root.insert(words[i].c_str());
    }

    for (int i = 0; i <= 17; i++) {
        if (root.find(words[i].c_str())) {
            cout << words[i] << "가 존재합니다." << endl;
        }
        else {
            cout << words[i] << "가 존재하지 않습니다." << endl;
        }
    }

    return 0;
}

결과

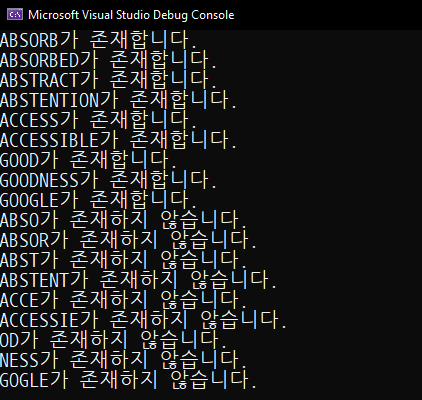
단점

Trie는 문자열 탐색에 있어 매우 빠른 속도를 가지지만 공간복잡도에 있어서는 접두사를 나타내는 모든 노드에서 포인터 배열을 가지므로 O(포인터 크기 * 자식 노드 배열 길이 * 트라이 노드의 총 개수)가 됩니다. 이를 감안하고 빠른 문자열 탐색이 필요한 경우 좋은 선택이 될 수 있습니다.

Trie 활용

Trie는 문자열의 Prefix를 판단하거나 탐색할때 매우 빠른 속도로 이용할 수 있습니다. 알고리즘 문제를 해결하기 위해서 사용되는 경우도 종종 있습니다. 예를 들어 아래의 백준 5052번 [전화번호 목록]에서 이용될 수 있습니다.

전화번호 목록 <- 백준 문제로 바로 가기

위 문제에서 Trie를 이용한 풀이가 궁금하다면 제 Github의 풀이를 참고해주세요.

#알고리즘 #자료구조

Follow @techbless

👈🏻 C++에서 CRT라이브러리로 메모리 누수확인하여 누수 없는 코드를 만들자

bits/stdc++.h 헤더파일로 알고리즘 문제 풀이 시간을 단축하는 방법 👉🏻