#알고리즘 #Computer Vision #Image Processing

RANSAC 알고리즘이란?

RANSAC(Random Sample Consensus) 은 데이터에서 발생하는 이상치(outlier) 에 매우 강력한(robust) 반복적 모델 추정 알고리즘입니다. 컴퓨터 비전에서 이미지 매칭, 기하학적 변환(호모그래피 등) 추정, 직선이나 원 같은 기하학적 모델 추정에 폭넓게 쓰입니다.

RANSAC 알고리즘의 주요 특징은 다음과 같습니다.

이상치(outlier)에 매우 강함 (Robustness)
최소한의 데이터만 사용하여 모델을 반복적으로 추정 (Minimal Sample Set)
무작위 샘플링 기반 접근 방식을 사용하여 반복적으로 최적 모델을 탐색

RANSAC 알고리즘의 작동 원리 및 과정 설명

RANSAC 알고리즘은 크게 다음과 같은 단계로 진행됩니다.

RANSAC을 이용한 라인 피팅 예시 (Halcon - 2D Metrology Recap) 포스트

1. 모델 정의 및 최소 데이터 개수 선정

먼저, 추정하고자 하는 모델을 정의하고, 이 모델을 결정짓기 위한 최소한의 데이터 개수를 정합니다.

직선(2점):
하나의 직선을 결정하기 위해서는 최소한 두 개의 점이 필요합니다. 직선 모델을 정할 때의 최소한의 데이터는 2점이 필요합니다.
호모그래피 행렬(4점):
호모그래피(homography)는 한 평면의 점들을 다른 평면으로 변환할 때 쓰이는 변환 행렬입니다. 호모그래피 행렬은 8개의 자유도(degree of freedom)를 가지기 때문에, 최소한 4쌍의 대응점이 필요합니다. 하나의 대응점(pair)은 2개의 방정식을 제공하며, 따라서 4개의 대응점은 8개의 방정식을 만들어 호모그래피를 정확히 결정할 수 있게 합니다.
원(3점):
원을 결정하려면 최소한 세 개의 점이 필요합니다. 따라서 원 모델의 최소 데이터 수는 3점입니다.

2. 랜덤 샘플링 및 임시 모델 추정

전체 데이터에서 무작위로 위에서 정의한 최소 개수만큼 샘플링합니다.
샘플링한 데이터를 기반으로 임시 모델을 추정합니다.

3. Inlier과 Outlier 구분

방금 추정한 임시 모델을 전체 데이터에 적용하여 잘 맞는 점을 Inlier, 맞지 않는 점을 Outlier으로 구분합니다.

4. 최적의 모델 선정 및 업데이트

위 과정을 반복하며 가장 많은 inlier을 포함하는 모델을 현재의 최적 모델로 기록하고 유지합니다.

5. 반복 종료 조건 확인

미리 정해진 반복 횟수를 초과하거나 원하는 정확도와 신뢰도를 얻으면 반복을 종료하고, 현재까지 얻은 최적의 모델을 최종 결과로 사용합니다.

위 과정을, 아래의 알고리즘 대로 수행하면, 최종 결과를 얻을 수 있습니다.

graph TD
    A[Start] --> B[데이터에서 임의 샘플 선택]
    B --> C[모델 생성]
    C --> D[모델에 맞는 데이터 포인트 찾기]
    D --> E[포인트가 모델에 적합한지 검증]
    E --> F{적합한 포인트가 일정 기준을 만족?}
    F -- 예 --> G[모델 개선]
    F -- 아니오 --> H[새로운 샘플 선택]
    G --> I{최적 모델 찾았나요?}
    I -- 예 --> J[알고리즘 종료]
    I -- 아니오 --> B
    H --> B

RANSAC 알고리즘의 수학적 표현과 예시

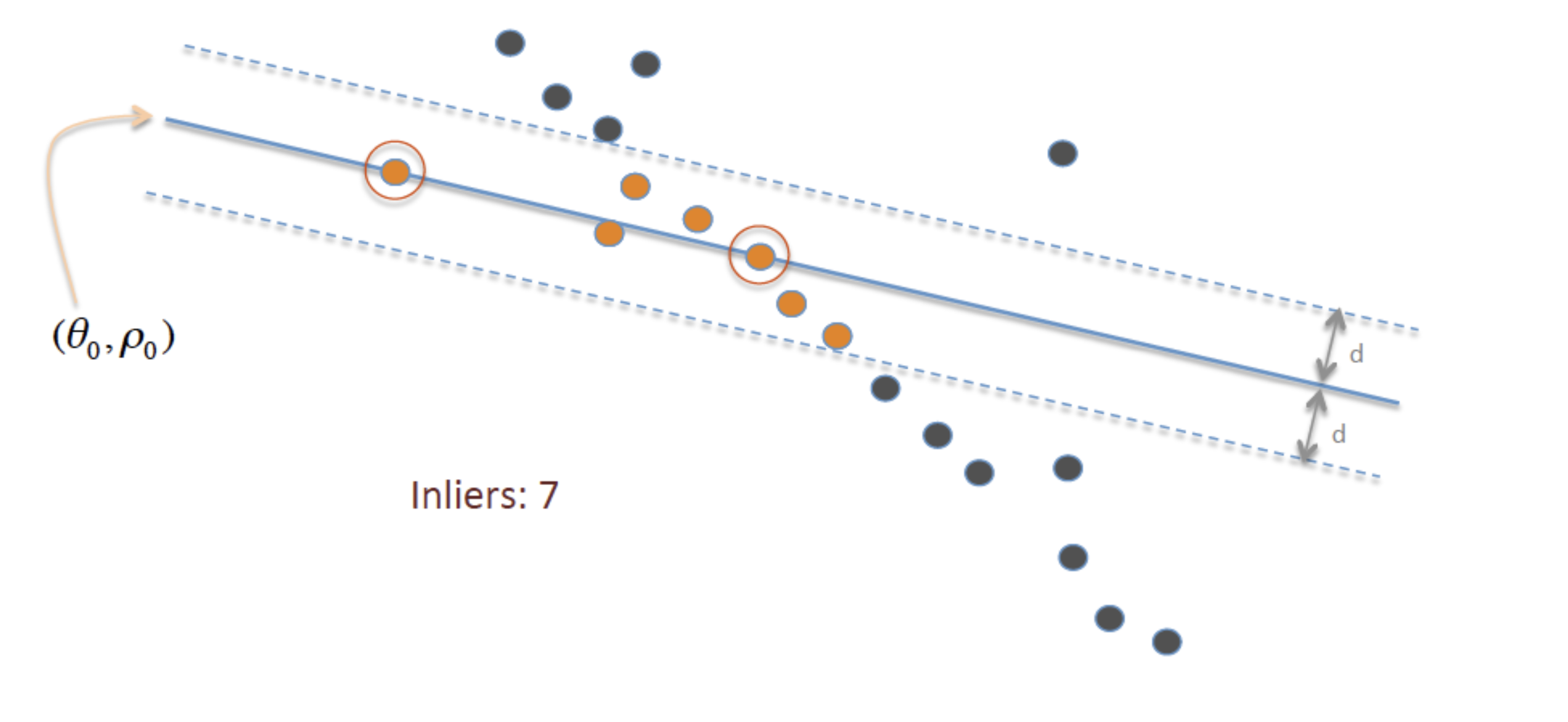
RANSAC의 가장 중요한 개념 중 하나는 Inlier 판별이며, 다음과 같은 수식으로 표현할 수 있습니다.

일반적으로 데이터 포인트 가 모델 의 내부점으로 판단되는 기준은 다음과 같습니다.

: 데이터 포인트 와 모델 간의 오차(거리)를 나타냅니다.
: 사용자가 정한 threshold이며, 실험적으로 설정됩니다.

직선 모델 예시

직선의 방정식을 다음과 같이 정의합니다.

이때 데이터 포인트 가 직선 모델과 얼마나 가까운지 나타내는 거리는 다음과 같습니다.

점과 직선사이 거리

이 값이 설정한 임계값 보다 작으면 내부점으로 간주됩니다.

알고리즘의 주요 파라미터와 설정법 (표 요약)

파라미터	설명	일반적 설정 방법
반복 횟수	샘플링과 모델 추정을 반복하는 횟수	데이터 내 이상치 비율에 따라 계산
임계값	내부점 판단 기준 (오차)	데이터 노이즈 및 실험적 판단
신뢰도	결과가 정확하다고 믿을 수 있는 확률 (95% 또는 99% 등)	일반적으로 0.95 또는 0.99 사용
내부점 비율	데이터 중 내부점 비율의 예상치	데이터 특성에 따라 실험적으로 결정

RANSAC의 반복 횟수 N 계산법

RANSAC의 반복 횟수() 계산식은 다음과 같은 확률 모델을 기반으로 합니다.

여기서 각 항의 의미는 다음과 같습니다.

: RANSAC이 최소 한 번 이상 올바른 모델을 찾을 확률(보통 0.95 또는 0.99로 설정) - 신뢰도
: 전체 데이터에서 outlier이 차지하는 비율.
: 전체 데이터에서 inlier이 차지하는 비율.
: 모델을 추정하는 데 필요한 최소 데이터 개수 (직선의 경우 2점, 호모그래피의 경우 4점 등).
: 반복 횟수(알고 싶은 값).

식의 의미:

은 무작위로 개의 데이터를 선택했을 때, 모두 내부점일 확률을 나타냅니다.
은 무작위로 선택한 데이터 중 적어도 하나 이상이 이상점일 확률입니다.
은 번 반복 시도했을 때, 모든 시도가 최소 하나의 이상점을 포함할 확률입니다.
따라서, 전체 식인 은 최소 한 번 이상 올바른 모델을 찾을 확률을 의미합니다.

이 식을 반복 횟수 에 대해 정리하면 일반적으로 사용하는 원하는 신뢰도를 얻기 위한 최소한의 반복 횟수를 이론적으로 결정하는 공식이 됩니다.

RANSAC 알고리즘 예시 코드 (Python, OpenCV 기준)

다음은 OpenCV와 Python을 이용해, 두 이미지 간 특징점 매칭에서 RANSAC을 활용하여 Homography 행렬을 구하는 예제 코드입니다.

import cv2  
import numpy as np  

# SIFT를 이용한 특징점 검출 및 descriptor 추출
sift = cv2.SIFT_create()  
kp1, des1 = sift.detectAndCompute(img1, None)  
kp2, des2 = sift.detectAndCompute(img2, None)  

# BFMatcher를 이용하여 두 이미지의 특징점 매칭 수행(k=2는 Lowe's ratio test를 위한 설정)
bf = cv2.BFMatcher()  
matches = bf.knnMatch(des1, des2, k=2)  

# Lowe's test로 좋은 매칭점 선별 (가장 유사한 매칭의 거리 차이가 명확한 특징점만 선택)
good_matches = [m for m, n in matches if m.distance < 0.75 * n.distance]

# 좋은 매칭점들에서 각 이미지의 좌표를 추출
src_pts = np.float32([kp1[m.queryIdx].pt for m in good_matches])  
dst_pts = np.float32([kp2[m.trainIdx].pt for m in good_matches])  

# RANSAC을 사용하여 호모그래피 행렬H를 추정하고, inlier을 판별하는 mask 반환
H, mask = cv2.findHomography(src_pts, dst_pts, cv2.RANSAC, 5.0)

여기서 사용된 threshold 5.0은 inlier을 판별할 때 허용 가능한 오차 범위이며, 실제 사용 환경과 데이터의 특성에 따라 조정할 수 있습니다. mask 배열은 RANSAC 알고리즘에서 내부점으로 분류된 매칭점을 나타내므로, 이후 모델을 더욱 정확하게 refine할 때 활용할 수 있습니다.